Cite as:
Bar-Yam, Y. (2026). Quantum Mechanics: Experiments, Assumptions, and a Unifying Physical Framework. Zenodo. https://doi.org/10.5281/zenodo.18248461, NECSI Technical Report 2026-01-01
We present a structured summary of an oscillatory-spacetime framework in which the standard formalism of quantum mechanics arises from a single physical assumption. In this approach, elementary particles are modeled as localized spacetime singularities carrying an intrinsic oscillatory degree of freedom. The persistence and transport of this oscillation account for wavefunction structure, superposition, energy–momentum relations, spin, relativistic dynamics, antiparticles, and electromagnetic interactions, without the introduction of independent postulates.
Quantum mechanics was constructed in response to a sequence of experimental results that revealed classically incompatible particle-like and wave-like properties. To account for these results, the standard formalism introduced a collection of distinct assumptions, including wave–particle duality, energy–frequency and momentum–wavelength relations, linear superposition, probabilistic measurement rules, operator-valued observables, and later relativistic extensions incorporating spin and antiparticles. These assumptions are extraordinarily successful, but they were introduced incrementally and are logically independent within the standard presentation.
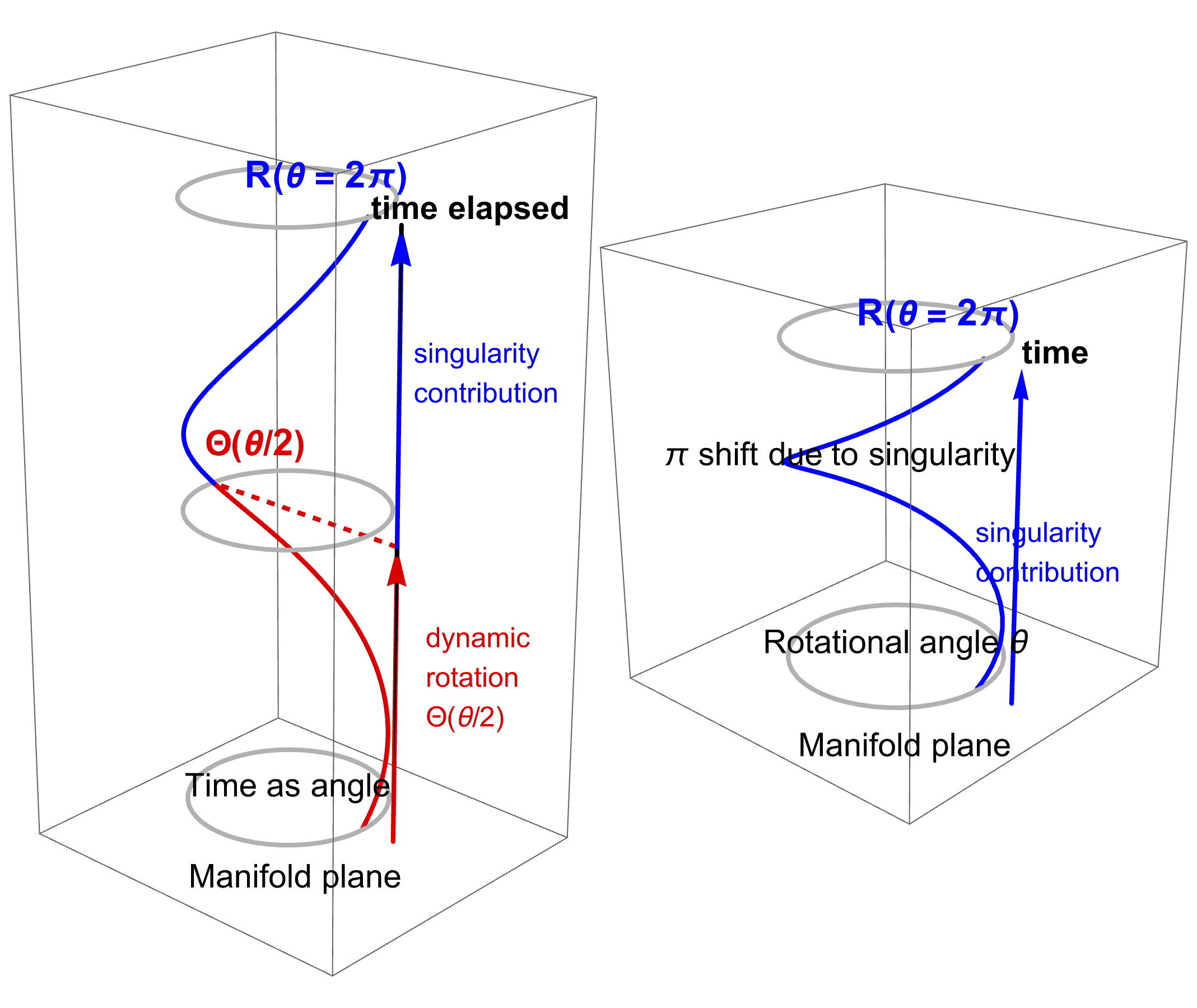
The key framing assumption of the oscillatory-spacetime approach is that the classical concept of a structureless point particle is replaced by a particle with an internal degree of freedom that gives rise to quantum behavior. Specifically, the framework assumes that elementary particles are localized spacetime singularities—understood as localized defects or distortions of spacetime continuity—carrying an intrinsic oscillatory degree of freedom, and that the familiar structures of quantum theory arise from the persistence of this internal dynamics in spacetime, even as the particle follows a definite trajectory. Under standard conditions, the oscillatory phase becomes the phase of the quantum wavefunction and is responsible for wave-like properties, while localized collisions can disrupt this persistence, giving rise to the phenomenology of discrete quantum measurement without invoking wave-function collapse.
The present paper summarizes the structure of this framework, the insights it provides, and the way in which quantum-mechanical assumptions are unified within it.
Fig 1. Rotational motion arising from a spacetime singularity.